SEISMIC MODELING OF DEEPWATER CHANNEL ELEMENTS

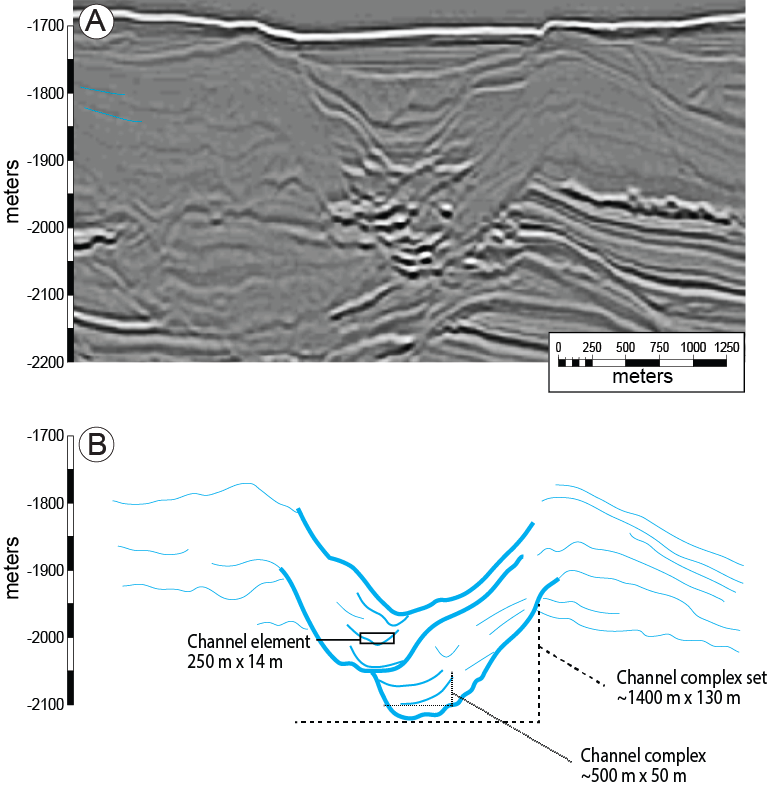
Problem Statement: Deepwater channel elements are fundamental building blocks of deepwater depositional system (Figure 1). Their internal architecture and variable stacking patterns generate variable net-to-gross distributions within channel systems and create tortuous fluid flow and connectivity pathways which impact hydrocarbon recovery.

Forward seismic modeling at the channel element scale can help to identify channel element fill and stacking pattern. The reflection character that we see in seismic is, in part, a function of the underlying stratigraphic architecture in these deepwater systems. My primary interest is to bridge the gap between architecture observed at outcrop observations and their analogous subsurface seismic responses. There has been a lot of work done in this area to qualitatively bridge this gap, but my interest is in taking it a step further to make a quantitative link.

Figure 1. (A) Seismic expression of deep-water channel-form hierarchy from the Dalia Field, West Africa (modified from Stevenson et al., 2015). Channel elements are readily characterized in outcrops, but generally below the resolution of seismic reflection data. Despite this, their internal architecture, as well as their stacking patterns, impart an important influence on deep-water channel reservoirs. Stacked channel elements compose a channel complex (examples defined by blue dashed lines), whereas stacked channel complexes compose a channel complex set, which is most readily differentiable in subsurface data (e.g., McHargue et al., 2011). (B) Sketch of high-amplitude core at the center of the example in Part A, highlighting the outlines of channel complexes (dashed blue lines in Part A). Hierarchical scales of wedge geometries from channel element, channel complex and channel complex set are indicated.

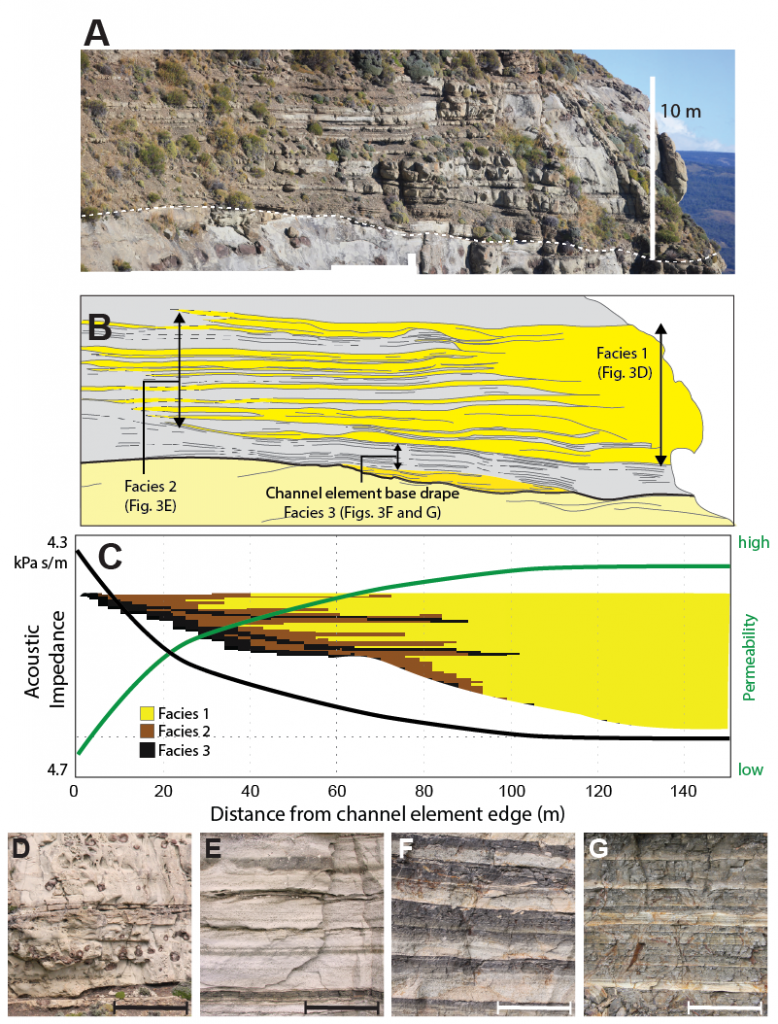
The outcrop expression of a single channel element show variations at the bed to geobody scale from thick-bedded and amalgamated sandstone to thin interbedded sandstone and mudstone (Figure 2). The rock properties assigned in this model assume low impedance sandstones and high impedance mudstone (after Stright et al., 2014; rock properties). The channel element modeled here is 250 m wide and 14 m thick.

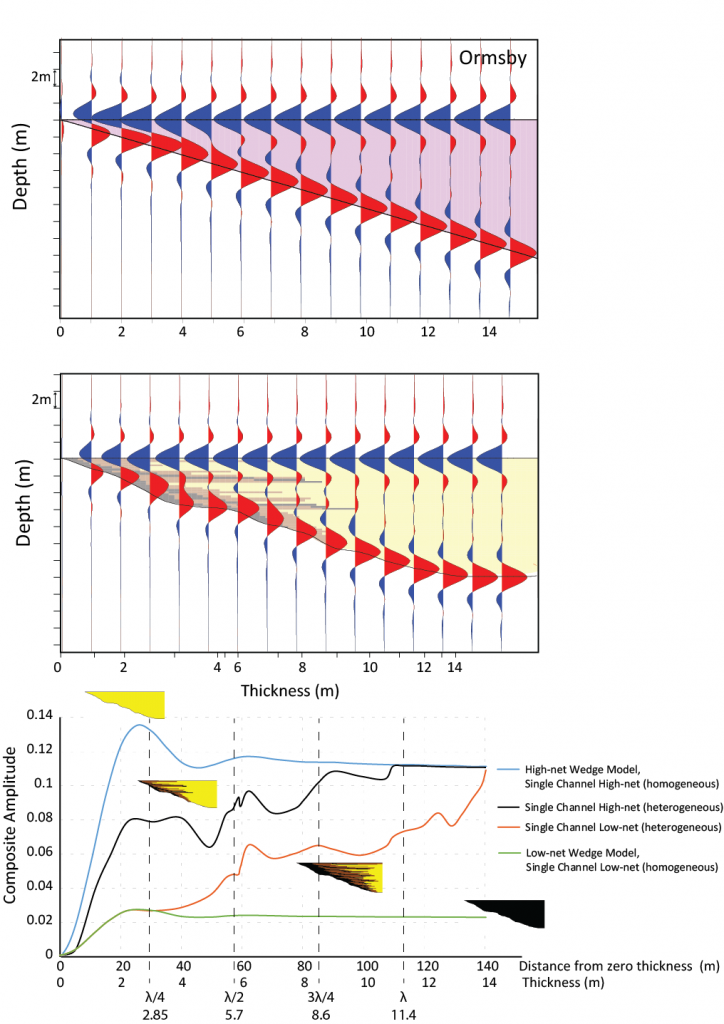
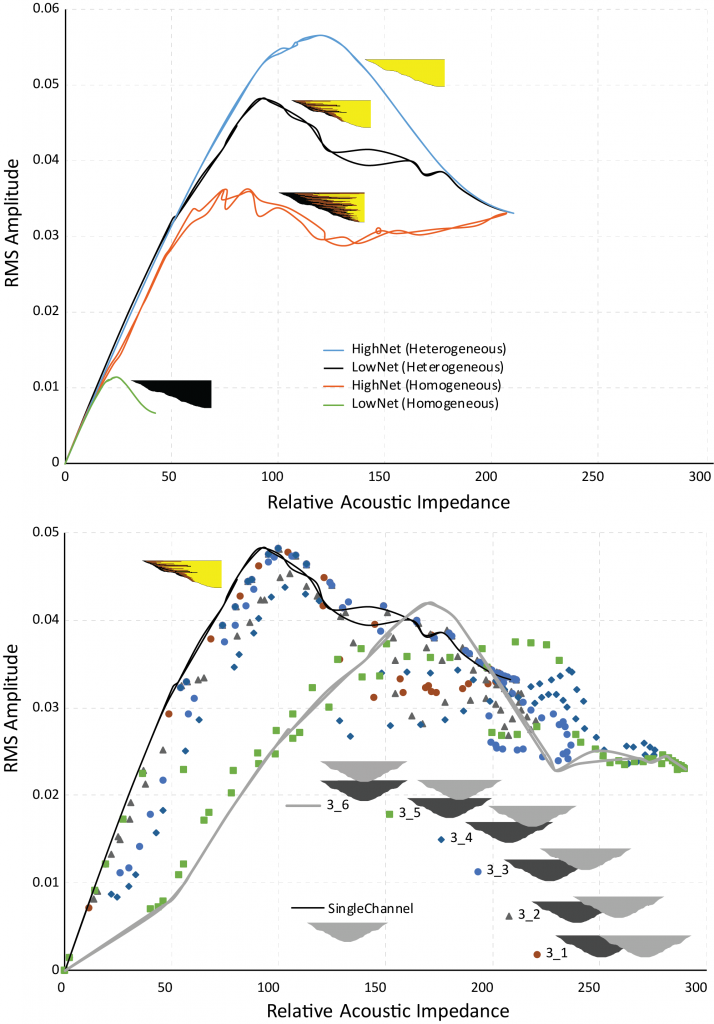
Figure 2. (A) Channel element axis (at right) to margin (at left) transition in outcrop, with line drawing of outcrop photo in (B). (C) Channel element cross-sectional template used to represent outcrop observations of intra-element architecture. Representative facies photos including: (D) thick-bedded sandstone of F1 (scale bar is 2 m long); (E) thick-bedded non-amalgamated sandstone of F2 (scale bar is 70 cm long); (F) thin-bedded sandstone and mudstone of F3a (scale bar is 20 cm long); and (G) thin-bedded mudstone with sandstone of F3b (scale bar is 20 cm long). Parts A-C modified from Jackson et al., 2019; Parts D-G from Meirovitz et al., in review.

The single channel element can be treated as a wedge and the first experiment was to understand how heterogeneity in the wedge impacted the amplitude response (Figure 3). The simple single channel element models

Figure 3. 180Hz single channel element and wedge models. End member high-net (yellow) and low-net (black) homogeneous wedge models bound the heterogeneous channel element wedges. The wavelet used here is an Ormsby wavelet (e.g., 60 Hz wavelet 4-12-90-140 and -90deg phase shift). The models have been converted to depth to be able to analyze them in units more familiar to an outcrop geologist. (Rock properties are from Stright et al., 2014; 60 Hz and 30 Hz tuning models were also generated)

Two or more channel element models can be combines with different stacking patterns and different fills to investigate the seismic response.

Research Questions: Can these simple channel element models be used as a foundation for quantitative interpretation? The goals would be to answer:

How many channel elements are there: 1 vs. 2 channel elements?
How are the channel elements stacked: laterally, vertically or in between?
What is the internal architecture of channel elements: homogeneous vs. heterogeneous, high-net vs. low net?

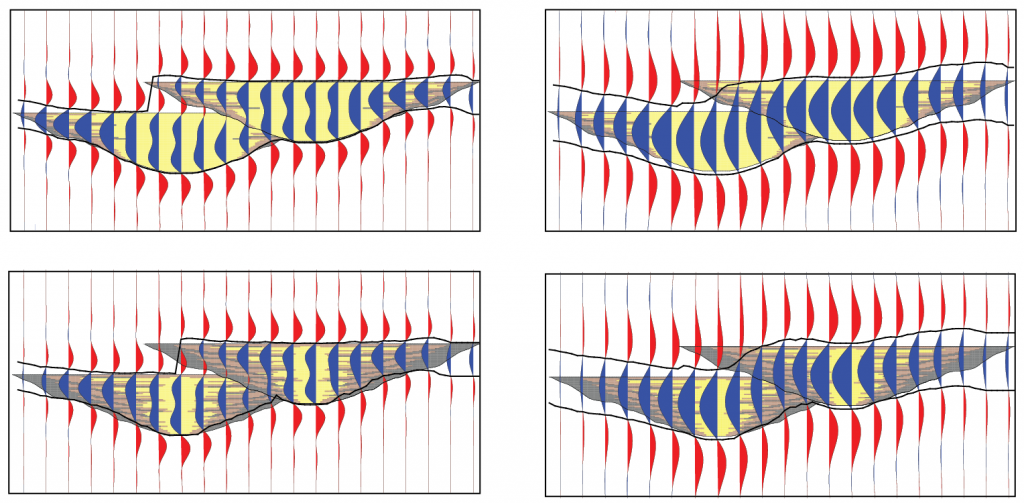
Figure 4. Examples of two channel element models. (A) 60 Hz, high-net heterogeneous, (B) 30 Hz, high-net heterogeneous, (C) 60Hz, low-net heterogeneous, and (D) 30 Hz, low-net heterogeneous. Models from Meirovitz et al., in review. All models for 60 and 30Hz are shown here.

My hypothesis is that by comparing 1) two channel model to a single channel model, and 2) homogeneously filled models to heterogeneously filled model, we might be able to say something about stacking patterns and fill. Furthermore, we could then apply what is learned in these small template-based models to a full scale field model to test out ability to differentiate numbers of elements, stacking patterns and fill. In my mind, this is a nice small test to scale up for interpretation workflows, analyzing inversion results, and understanding what machine learning approaches are actually classifying.

Plots that we have made to try to explore patterns in the data:

Interval attributes (RMS Amplitude) vs. apparent thickness
After the recent conversation on Sw.Ung I started playing around with sum of amplitudes from Relative Acoustic Impedance (RAI) and Cosine of Phase.
Interval attributes (RMS Amplitude) vs. true net thickness
Cross-plots of interval attributes (e.g., RMS Amplitude vs. sum of amplitudes from RAI)

Most of these plots are so noisy, that patterns are difficult to see.

Figure 5. (Top) Single channel element models cross-plot of RMS amplitude versus Relative Acoustic Impedance for all four homogeneous and heterogeneous cases. (Bottom) Heterogeneous high-net channel models. End members are the single channel element (orange) and two vertically stacked channel elements (gray; 3_6). The models transition from laterally stacked (red; 3_1) to vertically stacked (gray; 3_6).

If you were tackling this problem, what might you try?

Email me at lisa dot stright at colostate dot edu

References:

Jackson, A., Stright, L., Hubbard, S.M. and Romans, B.W., 2019. Static connectivity of stacked deep-water channel elements constrained by high-resolution digital outcrop models. AAPG Bulletin, 103(12), pp.2943-2973. https://doi.org/10.1306/03061917346

McHargue, T., Pyrcz, M.J., Sullivan, M.D., Clark, J.D., Fildani, A., Romans, B.W., Covault, J.A., Levy, M., Posamentier, H.W. and Drinkwater, N.J., 2011. Architecture of turbidite channel systems on the continental slope: patterns and predictions. Marine and Petroleum Geology, 28(3), pp.728-743. https://doi.org/10.1016/j.marpetgeo.2010.07.008

Stevenson, C.J., Jackson, C.A.L., Hodgson, D.M., Hubbard, S.M. and Eggenhuisen, J.T., 2015. Deep-Water Sediment BypassDEEP-WATER SEDIMENT BYPASS. Journal of Sedimentary Research, 85(9), pp.1058-1081. https://doi.org/10.2110/jsr.2015.63

Stright, L., Stewart, J., Campion, K. and Graham, S., 2014. Geologic and seismic modeling of a coarse-grained deep-water channel reservoir analog (Black’s Beach, La Jolla, California) Seismic Modeling of a Deep-Water Reservoir Outcrop Analog, California. AAPG bulletin, 98(4), pp.695-728. https://doi.org/10.1306/09121312211