F 321 – Assignment #5
Forest Products, Log Rules, and Stratification
Objective: This assignment will ask you to work with units, conversions, and quantitative approaches that are specific to summarizing wood quantity in logs and processed lumber. Additionally, you will explore the use of stratified sampling in forest inventories.
Student Learning Outcomes: Upon completing this assignment you should be able to:
- Apply log rules and understand why they provide different results.
- Allocate samples across a stratified sampling design
- Explain the statistical and financial benefits of stratification.
- Summarize and critique a stratified sampling design for effectiveness.
- Derive your confidence in population parameters from a stratified sampling design.
1. Compute the total volume and total value for these items of lumber, assume we get 12 bf per cu ft:
a) 136 pieces 3 in x 6 in. x 16 ft @ $228.50 per MBF
b) 254 pieces 2 in x 8 in. x 18 ft @ $336.00 per MBF
c) 346 pieces 4 in x 4 in. x 20 ft @ $232.45 per MBF
2. Calculate the volume in standard cords for the following stacks of wood:
a) 20 ft x 80 ft x 4 ft
b) 12 ft x 32 ft x 5 ft
c) 16 ft x 32 ft x 10 ft
d) 50 ft x 80 ft x 10 ft
3. Compute the log volume (in cubic feet) for the following logs using EACH of the Huber’s, Smalian’s, Newton’s, the 2-End Conic Rule, and the subneiloid rule formulas (assume inside bark for all measurements): [Must show each equation’s setup at least once]
a) Small end diameter = 6.2 in
Midpoint diameter = 7.6 in
Large end diameter = 9.0 in
Length = 16 ft
b) Small end diameter = 24.0 in
Midpoint diameter = 26.4 in
Large end diameter = 28.7 in
Length = 32 ft
c) Small end diameter = 10.5 in
Midpoint diameter = 11.0 in
Large end diameter = 11.6 in
Length = 8 ft
4. Calculate the mean and standard deviation for the value of logs a-c across the 5 calculation methods, assuming $4.11 per cubic foot. Which log produced the least variability and why?
5. You are selling firewood and know that the species you are working with has an average oven-dried wood density of 0.48 g (cm3). From knowing that the wood you are working has a moisture content of 105%, that there is 75 ft3 of solid wood per cord, and the weight of bark is 800 pounds per cord, what is the weight, in pounds, of the average cord?
6. If the allowable error is given as a percent what measure of variation would you use to calculate sample size? Assume no calculation other than the sample size calculation.
7. What is stratified random sampling and what are three reasons we use it?
8. What are the steps in the stratification process?
9. What are the three types of allocation in stratified random sampling, provide their formulas and define their parameters?
10. You are given the following stand information and told to allocate 160 – 1/10 acre plots. Calculate how many plots you would allocate to each strata using proportional allocation.
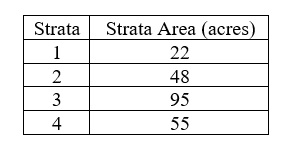
11. Now allocate the 160 plots using Neyman allocation.
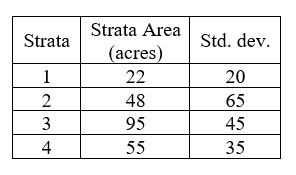
12. Calculate the strata mean and variance per acre from the plot-level volumes (cu ft) inventoried in the cruise performed using stratified sampling of 1/10 acre plots, each strata is 40 acres in size. Assume sampling without replacement. Does this seem to be a good stratification of the population? Explain your answer.
13. Calculate the following combined statistics for the cruise in question #12, assuming sampling without replacement.
Combined mean per acre:
Combined variance per acre:
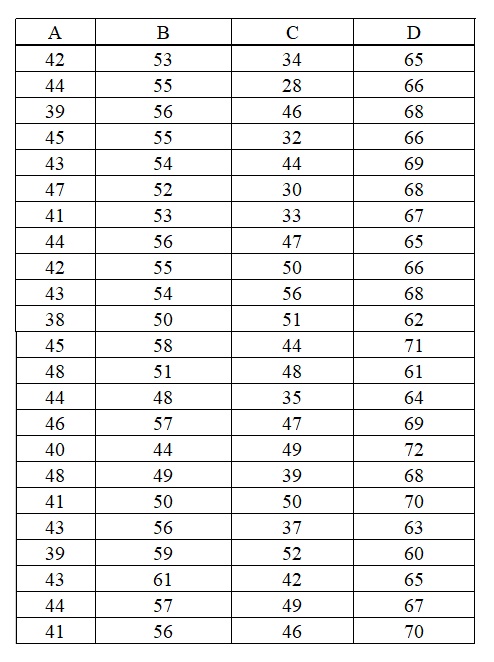
14. Using your calculations from question #13 and what you know from question #12, compute the 90% confidence interval for the revenue you can expect to earn for harvesting all of your land. You are able to get a price of $3.11 cu ft.
Extra Credit (5 points):
If you decide to harvest only Strata B from question #12, what would be the maximum revenue you would expect if the stand consisted of 80% fir and 20% pine and you received $2.48 cu ft for fir and $2.27 cu ft for pine? Use a 90% confidence level.
