As discussed in class, we frequently want to quantify autocorrelation for single variables across multiple samples. Like we have talked about for different data types, the degree of spatial autocorrelation in a dataset can allow us to develop hypothesis about the controlling factors that generated the pattern. Here we are talking about understanding how spatial autocorrelation manifests in either lattice or polygon data types.

Objectives:  The goal of today’s lab is to learn how to explore spatial autocorrelation on areal data in R.

The R Package:  Today we will be using the R package raster, which provide functions for basic analysis of lattice data.

The datasets: Today you be working with a dataset called PFDP_BA.asc, which is a raster grid (10 m spatial resolution) depicting the basal area of all tree species across the Pike’s Peak Forest Dynamics Plot outside of Woodland Park, CO.

Save the PFDP_BA.asc file from Canvas to an appropriate location.

---

Exercise 1 – Global Spatial Autocorrelation

Moran’s I and Geary’s C are two techniques that can be used to calculate spatial correlation from areal data. They essential calculate the correlation between nearby locations in space. Both techniques can be used to calculate global and local estimates of spatial autocorrelation. The local estimates are often used to identify spatial clustering (i.e. hotspots) and outliers in attribute values. In general, positive values for I and C indicate that the feature is surrounded by features with similar values (i.e. a spatial cluster), while negative values indicate that the feature is surrounded by features with dissimilar values (i.e. a spatial outlier).
When working with polygon data the I and C statistics are calculated on polygon centroids with a proximity weighting scheme (spatial weights matrix) to account for geometric irregularities between polygons. When working with lattice data image windows are used to develop the spatial weights matrix. There are typically two forms of windows used for the weight matrix, the Queen filter and the Rook filter; however, any filter could be used.

The goal of today’s lab is to detect spatial clusters of grand fir age from the datasets using Moran’s I and Geary’s C.

Today’s lab will be conducted using the raster and spdep R package.

1. Start R
2. Download and Install the raster package from CRAN
3. Load the raster package:

> require(raster)

4. Read the PFDP_BA.asc file into R. The PFDP_BA.asc file in an ASCII raster file that was exported from ArcMap using the ‘grid to ascii’ conversion tool. This file can be read into R by setting the working directory (this is the location where you saved the PFDP_BA.asc file) by filling in the following commands:

> setwd(‘insert/path/to/file/’)

Read in the PFDP_BA.asc file to a raster object:

> r.pfdp = raster(‘PFDP_BA.asc’)

Plot the PFDP BA raster

> plot(r.pfdp)

This map displays total basal area per hectare across the Pike’s Peak Forest Dynamics Plot. The spatial resolution is 10 m. The UTM coordinates are displayed on the y and x axes. As you can see the basal area ranges between 0 and ~100 square meters per hectare.

5. Calculate Global Moran’s I and Geary’s C values on the full dataset.

Below we will use a few commands to create new rasters storing Moran’s I and Geary’s C values for a 3×3 queen weighting filter, but first we need to create the weighting matrix:

> queen <- matrix(c(1, 1, 1, 1, 0, 1, 1, 1, 1), 3, 3)

Moran’s I with our 3×3 queen filter:

> m.3.q = Moran(r.pfdp, w = queen)
> m.3.q

Geary’s C with a 3×3 queen filter:

> g.3.q = Geary(r.pfdp, w = queen)
> g.3.q

What do these value for global Moran’s I and Geary’s C indicate? _________________________

Now run the local version of these functions and plot the results:

> par(mfrow=c(2,1), omi=c(0, 0, 0, 0), mai=c(0.4, 0.4, 0.3, 0.1))
> ml.3.q = MoranLocal(r.pfdp, w = queen)
> plot(ml.3.q, main=”PFDP BA – Moran’s I”, cex.axis = 0.75, cex.main = 0.75)

Geary’s C with a 3×3 queen filter:

> gl.3.q = GearyLocal(r.pfdp, w = queen)
> plot(gl.3.q, main=”PFDP BA – Geary’s C”, cex.axis = 0.75, cex.main = 0.75)
> par(mfrow=c(1, 1))

What do you notice about the maps of local indices values compared to the global values?
______________________________________________________________________________
______________________________________________________________________________

What are the omi and mai parameters doing in the par command? _________________________
______________________________________________________________________________

6. Subset the dataset to a smaller spatial extent.

It would be interesting to play around with a few different filter sizes and configurations, but at this scale any differences would be hard to see. A solution is to create a spatial subset of the data so we can more easily visualize the results. We can use the crop command to do this.

Set the cropping extent by defining the min-x, max-x, min-y, and max-y for a 250m x 250m area of the PFDP BA dataset:

> e = extent()

Crop the raster

> r.pfdp.crp = crop(r.pfdp, e)

Plot the cropped raster

> plot(r.pfdp.crp)

Determine what the min, max, and median of the basal area per hectare in the cropped raster:

min: _______    max: _______    median: _______

7. Calculate the Global and Local Moran’s I and Geary’s C values on the subset dataset.

Moran’s I with a 3×3 queen filter

> m.3.q.sub = Moran(r.pfdp.crp, w = queen)
> ml.3.q.sub = MoranLocal(r.pfdp.crp, w = queen)

Plot the result

> plot(ml.3.q.sub)

Geary’s C with a 3×3 queen filter

> g.3.q.sub = GearyLocal(r.pfdp.crp, w = queen)
> gl.3.q.sub = GearyLocal(r.pfdp.crp, w = queen)

Plot the result

> plot(gl.3.q.sub)

Plot the original map and both results on the same figure:

> op = par(mfrow = c(1, 3) , mai = c(0.4, 0.4, 0.5, 0.4))
> plot(r.pfdp.crp, main = ‘PFDP BA’)
> plot(ml.3.q.sub, main = ‘Local Morans-I’)
> plot(gl.3.q.sub, main = ‘Local Gearys-C’)

Describe any differences in the results. Do either show spatial clustering of basal area at the PFDP?
______________________________________________________________________________
______________________________________________________________________________
______________________________________________________________________________

8. Experiment with different filter sizes and configurations.

So far, we have only been using a 3×3 queen filter to weigh neighboring pixels. Essentially any logical filter size and configuration could be used. The rook filter is very commonly used.

Look back at how we created the queen filter and use that to fill in the following matrix command to construct a rook filter:

> rook = matrix()

Look at the rook filter:

> rook

As you can see from the result, the rook filter weights pixels in the four cardinal directions equally and does not incorporate pixel values off the diagonal.

3×3 global and local Moran’s I with the rook filter:

> m.3.r.sub = Moran(r.pfdp.crp, w = rook)
> ml.3.r.sub = MoranLocal(r.pfdp.crp, w = rook)

Compare Moran’s I results between 3×3 queen and rook filters

> op = par(mfrow = c(1, 3))
> plot(r.pfdp.crp, main = “PFDP BA”)
> plot(ml.3.q.sub, main = “Local Moran’s I – Queen”)
> plot(ml.3.r.sub, main = “Local Moran’s I – Rook”)

Turn this plot in with your lab.

3×3 global and local Geary’s C with the rook filter

> g.3.r.sub = Geary(r.pfdp.crp, w = rook)
> gl.3.r.sub = GearyLocal(r.pfdp.crp, w = rook)

Compare C results between 3×3 queen and rook filters

> op = par(mfrow = c(1, 3))
> plot(r.pfdp.crp, main = “PFDP BA”)
> plot(gl.3.q.sub, main = “Local Geary’s I – Queen”)
> plot(gl.3.r.sub, main = “Local Geary’s I – Rook”)
> par(mfrow = c(1,1))

Turn this plot in with your lab.

Looking at your global values, what do you notice is the change by using the rook instead of the queen weighting filter?
_____________________________________________________________________________
_____________________________________________________________________________

Looking at your maps, which index seems to be more sensitive to changes in the weighting filter? Why do you think this is?
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________

For me the difference in weighting filters is more pronounced in the Geary’s C maps.

Feel free to experiment with different filter sizes and configurations. The queen filter size can be changed by altering the ‘w = 3’ portion of the GearyLocal and MoranLocal commands. For example, to specify a 7X7 queen filter simply set ‘w = 7’.

Here is an example of how to use the matrix command to make a 5X5 filter with a circular weighting function.

If you want your filter to look like this:

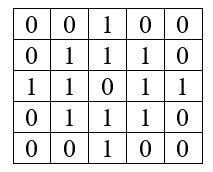
Type the following:

> f = matrix(c(0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0), nrow = 5)

To use it simply set ‘w = f’

> gl.5.r.sub = GearyLocal(r.abgr.crp, w = f)
> plot(gl.5.r.sub)

What do you get for the global Moran’s I and Geary’s C if you use a 5×5 queen weighting filter on the entire dataset?

Moran’s I: ____________                  Geary’s C: ____________

Run your 5×5 queen weighting filter for local Moran’s I on the entire PFDP_BA dataset.

Turn this map in with your lab.

Do you notice any obvious clustering? Do these correspond to high or low basal area values?
______________________________________________________________________________
______________________________________________________________________________