Population Viability Analysis

Viability of a Population

Slide 2 of 47

The viability of a population is defined as the probability that it will not go extinct during a fixed time span given the current population size.

Determining Viability of a PopulaSlide 3 of 47Two procedures are commonly used for evaluating the viability of a population, or the probability that the population will survive for some time. Population viability analysis (PVA) is the methodology of estimating the probability that a population of a specified size will persist for a specified length of time. The minimum viable population (MVP) is the smallest population size that will persist some specified length of time with a specified probability. In the first case, the probability of extinction is estimated, whereas in the second, the number of animals is estimated that is needed in the population to meet a specified probability of persistence. For a population that is expected to go extinct, the time to extinction is the expected time the population will persist. Both PVA and MVP require a time horizon, i.e., a specified, but arbitrary, time to which the probability of extinction pertains.

Population Persistence

Slide 4 of 47

Qualitatively, population biologists know a considerable amount about what allows populations to persist. Some generalities about population persistence are provided by Ruggiero et al. 1994. Typically, recovery plans for an endangered species try to 1) create multiple populations of the species, so that a single catastrophe will not wipe out the entire species, and 2) increase the size of each population so that genetic, demographic, and normal environmental uncertainties are less threatening (Meffe and Carroll 1994:191-192). However, Hess (1993) argues that connected populations can have lower viability over a narrow range in the presence of a fatal disease transmitted by contact. He demonstrates the possibilities with a model, but doesn’t have data to support his case. However, the point he makes seems biologically sound, and the issue can only be resolved by optimizing persistence between these two opposing forces. Spatial variation, i.e., variation in habitat quality across the landscape, affects population persistence. Typically, extinction and metapopulation theories emphasize that stochastic fluctuations in local populations cause extinction and that local extinctions generate empty habitat patches that are then available for recolonization. Metapopulation persistence depends on the balance of extinction and colonization in a static environment (Hanski 1996). For many rare and declining species, Thomas (1994) argues (1) that extinction is usually the deterministic consequence of the local environment becoming unsuitable (through habitat loss or modification, introduction of a predator, etc.); (2)€that the local environment usually remains unsuitable following local extinction, so extinctions only rarely generate empty patches of suitable habitat; and (3) that colonization usually follows improvement of the local environment for a particular species (or long-distance transfer by humans). Thus, persistence depends predominantly on whether

Population Persistence

Slide 5 of 47

Successional stage affects the persistence of a population. Later seral stages are more likely to persist than early seral stages. Hence, plant and animal populations that make up the community will have longer persistence times if the community is a long-lived seral stage.

Population Persistence

Slide 6 of 47

Foley (1994) uses a model to agree with 5 above, that populations with higher reproductive rates are more persistent. However, mammals with larger body size can persist at lower densities (Silva and Downing 1994), and typically have lower annual and per capita reproductive rates. The predicted minimal density decreases as the -0.68 power of body mass, likely because of less variance in reproduction relative to life span.

Population Persistence

Slide 7 of 47

The last item on the Ruggiero et al.’s 1994 list suggests that increased variation in time leads to lower persistence (Shaffer 1987, Lande 1988, 1993). One reason that increased temporal variation causes lowered persistence is that catastrophes, such as hurricanes, fires, or floods are more likely to occur in systems with high temporal variation. Populations in the wet tropics can apparently sustain themselves at densities much lower than those in temperate climates, likely because of less environmental variation. Basically the distinction between a catastrophe and a large temporal variance component is arbitrary, and on a continuum. Further, even predictable effects can have an impact. Beissinger (1995) models the effects of periodic environmental fluctuations on population viability of the snail kite (€Rostrhamus sociabilis€).

Sources of Variation

Slide 8 of 47

The persistence of a population depends on stochasticity, or variation. Sources of variation, and their magnitude, determine the probability of extinction, given the population growth mechanisms specific to the species. The total variance of a series of population measurements is a function of process variation (stochasticity in the population growth process) and sampling variation (stochasticity in measuring the size of the population). Process variation is a result of demographic, temporal and spatial (environmental variation), and individual phenotypic and genotypic) variation. In this section, I will define these sources of variation more precisely, and I will develop a simple mathematical model to illustrate these various sources of stochasticity, thus demonstrating how stochasticity affects persistence.

Naive Population Model

Slide 9 of 47

Consider a population with no variation, one that qualifies for the simple, density-independent growth model €N€t + 1€€ = €N€t€€(1 + €R€), where €N€t€€ is the population size at time €t€ and €R€ is the finite rate of change in the population. This model is deterministic, and hence, so is the population. €R€€€€0 guarantees that the population will persist, in contrast to €R€€<�0, which guarantees that the population will go extinct (albeit in an infinite amount of time, because a fraction of an animal is allowed in this model). �R� can be considered to be a function of birth and death rates, so that �R��=”€€b€€-€€d€” defines the rate of change in the population as a function of birth rate (�b�) and death rate (�d�). When the birth rate exceeds or equals the death rate, the population will persist with probability 1 in this deterministic model.

Deterministic Population Growth

Slide 10 of 47

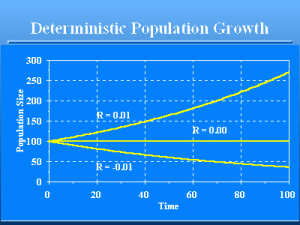
Deterministic model of population growth. For values of €R€ € 0, the population persists indefinitely. For values of R <0, the population will eventually go extinct in that the number of animals will approach zero.

Stochastic Population Model

Slide 11 of 47

Lets extend this naive model by making it stochastic. I will change the parameter €R€ to be a function of 2 random variables. At each time €t€, I determine stochastically the number of animals to be added to the population by births, and then the number to be removed by deaths. Suppose the birth rate equals the death rate, say €b€€=€€d€€=€0.5. That is, on average 50% of the €N€t€€ animals would give birth to a single individual and provide additions to the population, and 50% of the €N€t€€ animals would die and be removed from the population. Thus, the population is expected to stay constant, because the number of births equals the number of deaths. A reasonable stochastic model for this process would be a binomial distribution. For the binomial model, you can think of flipping a coin twice for each animal. The first flip determines if the animal gives birth to 1 new addition to the population in €N€t+1€€, and the second flip determines if the animal currently a member of €N€t€€ remains in the population for another time interval to be a member of €N€t+1€€, or dies. If we start with €N€0€€€=€100, what is the probability that the population will persist until €t€€=€100?

Demographic Variation

Slide 12 of 47

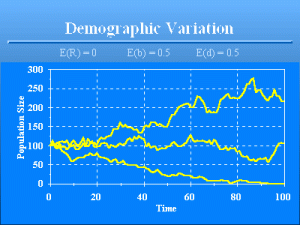
You might be tempted to say the probability is 1 that the population will persist until €t€€=€100 because the expected value of €R€ is 0 given that the birth rate equals the death rate, i.e., E(€R€)€=€0, so that E(€N€t+1€€)€=€E(€N€t€€). You would be wrong! The graph shows three examples of the outcome of the population model with only demographic variation. The lower population goes extinct at time 93. Birth and death probabilities are both 0.5, making the expected value of €R€ = 0. The type of stochasticity illustrated by this model is known as €demographic variation€. I like to call this source of variation “penny flipping variation” because the variation about the expected number of survivors parallels the variation about the observed number of heads from flipping coins. To illustrate demographic variation, suppose the probability of survival of each individual in a population is 0.8. Then on average, 80% of the population will survive. However, random variation precludes exactly 80% surviving each time this survival rate is applied. From purely bad luck on the part of the population, a much lower proportion of the population may survive for a series of years, resulting in extinction. Because such bad luck is most likely to happen in small populations, this source of variation is particularly important for small populations, and hence the name demographic variation. The impact is small for large populations. As the population size becomes large, the relative variation decreases to zero. That is, the variance of €N€t+1€€/€N€t€€ goes to zero as €N€t€€ goes to infinity. Thus, demographic variation is generally not an issue for persistence of larger populations.

Persistence vs. Initial Pop. Si

 Slide 13 of 47

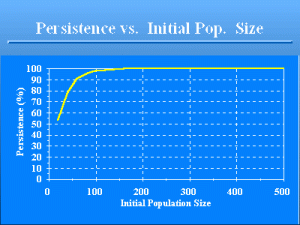
Implementation of this model on a computer shows that the probability of persistence is 98.0%, i.e., 2.0% of the time the population does not persist for 100 years without €N€t€€ becoming 0 for some €t€. . These estimates were determined by running the population model 10,000 times, and recording the number of times the simulated population went extinct before 100 years had elapsed. Lowering the initial population to €N€0€€€=€20 results in persistence of only 53.2% of the populations, again based on 10,000 runs of the model. Setting €N€0€€€=€500 improves the persistence rate to nearly 100%. Note that the persistence is not linear in terms of €N€0€€ . Initial population size has a major influence on persistence.

Temporal Variation

 Slide 14 of 47

Another way to decrease persistence is to increase the stochasticity in the model. One way would be to introduce €temporal variation€ by making €b€ and €d€ random variables. Such variation would be exemplified by weather in real populations. Some years, winters are mild and survival and reproduction are high. Other years, winters are harsh and survival and reproduction are poor. To incorporate this phenomena into our simple model, suppose that the mean birth and death rates are again 0.5, but the values of the birth rate and the death rate at a particular time €t€ are each selected from a statistical distribution, say a beta distribution. That is, each year, new values of €b€ and €d€ are selected from a beta distribution.

Beta Distribution

Slide 15 of 47

The beta distribution is described by 2 parameters, € > 0 and € > 0. The mean of the distribution is given by €/(€ + €) and the variance as €€/[(€€+€€)€2€(€€+€€€+€1)], with the mode (€ – 1)/(€ + € – 2) (mode only for € € 1). Most random number generation techniques for the beta distribution require you to specify values for € and €. For a given mean (�) and variance (€€2€) or standard deviation (€), stackalign{ alpha ~=&~ {mu sup 2 (1~-~mu)} over {sigma sup 2} ~-~ mu , ~ func { a n d } # beta ~=&~ {left ( sigma sup 2 ~+~ mu (mu ~-~ 1) right ) (mu ~-~ 1)} over { sigma sup 2 } ~. } However, the amount of variation possible is limited because the distribution is bounded on the [0,1] interval. Thus, for a mean of 0.5, the maximum variance approaches 0.25 as € and € approach zero.

Beta Distribution Examples

Slide 16 of 47

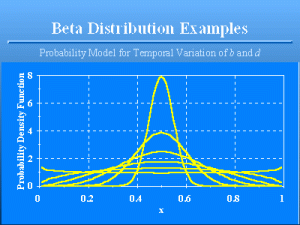
Examples of the beta distribution, all with mean 0.5. The standard deviations proceeding from the tallest curve to the lowest curve at €x€ = 0.5 are 0.05 to 0.3 in increments of 0.05.

Persistence with Temporal Variati

Slide 17 of 47

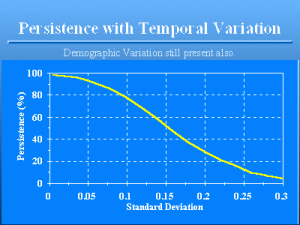
The standard deviation of the birth and death rates over time affect persistence because these values determine the standard deviation of €R€. The smaller the standard deviations, the more the model approaches the demographic variation case, and thus, as €N€t€€ approaches infinity, the deterministic case. As the standard deviation increases, the more the variation in €N€t€€, regardless of population size, and the less likely the population is to persist. Thus, a standard deviation of 0.2 for both the birth and death rates results in only 28.5% persistence for €N€0€€€=€100. Compare this to the 77.4% persistence achieved for a standard deviation of 0.1, or to the 98.0% persistence when no variation in birth and death rates occurred but demographic variation is still present. This second source of variation in our simple model is €temporal variation€, i.e., variation in the parameters of the model across time. As the example shows, increasing temporal variation decreases persistence. The simple model illustrated assumed that no correlation existed between the birth rate and the death rate, i.e., that the 2 rates were independent. However, in real populations, there is likely a high correlation between birth rates and death rates across years. Good years with lots of high quality resources available to the animals probably result in increased reproduction and survival, whereas bad years results in poor reproduction and high mortality. Including a negative covariance of birth and death rates (or a positive covariance between birth and survival rates) in the model results in an even bigger impact of temporal variation on persistence. That is, the bad years are really bad because of both poor reproduction and high mortality, and the good years are really good. The net effect of this negative covariance of birth and death rates is to decrease persistence.

Spatial Variation

Slide 18 of 47

€Spatial variation€ is the variation across the landscape that is normally associated with populations. Factors causing geographic variation include geologic differences that affect soil type, and thus habitat, and weather patterns, e.g., differences in rainfall across the landscape. If the immigration and emigration rates are high across the landscape, so that subpopulations that are depleted because of local conditions, high spatial variation can lead to higher persistence. This is because the probability of all the subpopulations of a population being affected simultaneously by some catastrophe is low when high spatial variation exists. In contrast, with low spatial variation, the likelihood of a bad year affecting the entire population is high. Thus, in contrast to temporal variation, where increased variation leads to lowered persistence, increased spatial variation leads to increased persistence given that immigration and emigration are effectively mixing the subpopulations. If immigration and emigration are negligible, then spatial variation divides the population into smaller subpopulations, which are more likely to suffer extinction from the effect of demographic variation on small populations.

Environmental Variation

Slide 19 of 47

The combination of temporal and spatial variation is termed €environmental variation€. Both dictate the animal’s environment, one in time, one in space.

Individual Variation

Slide 20 of 47

All the models examined so far assume that each animal in the population has exactly the same chance of survival and reproducing, even though these rates are changing with time. What happens if each animal in the population has a different rate of survival and reproduction? Differences between the individuals in the population are termed individual heterogeneity, and creates €individual variation€. Many studies have demonstrated individual heterogeneity of individual survival and reproductions, e.g., Clutton-Brock (1982) demonstrated lifetime reproductive success of female red deer (€Cervus elaphus€) varied from 0 to 13 calves reared per female. Differences in the frequency of calf mortality between mothers accounted for a larger proportion of variance in success than differences in fecundity. Bartmann et al. (1992) demonstrated that overwinter survival of mule deer fawns was a function of the fawn’s weight at the start of the winter, with larger fawns showing better survival. Individual variation is caused by €genetic variation€, i.e., differences between individuals because of their genome. However, €phenotypic variation€ is also possible. Animals that endure poor nutrition during their early development may never be as healthy and robust as animals that are on a higher nutritional plane, even though both are genetically identical. Animals with access to more and better resources have higher reproductive rates, e.g., red deer (€Cervus elaphus€) (Clutton-Brock et al. 1982). Thus, individual heterogeneity may result from both genetic and phenotypic variation. €omnicki (1988) develops models of resource partitioning that result in phenotypic variation of individuals.

Simulation of Individual Variatio

Slide 21 of 47

To illustrate individual variation, start with the basic demographic variation model developed above. Instead of each animal having exactly a birth rate of 0.5 and a death rate of 0.5, lets select these values from beta distributions with a mean of 0.5. The birth and death rates assigned to an animal remain for its life time. As new animals are added to the population, they likewise are assigned life-time birth and death rates. How does persistence of this new model compare with the results from the demographic model?

Individual Variation

Slide 22 of 47

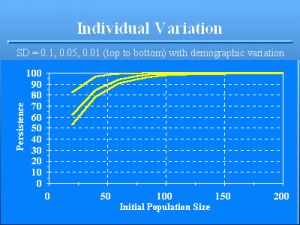
Effect of individual variation on population persistence. The 3 lines from top to bottom have standard deviations of 0.1, 0.05, and 0.01 for the birth and death rates. Compare these results with previous graph where only demographic variation was present, i.e., where the standard deviation of individual variation is zero. The reason that increased individual heterogeneity increases population persistence is that increased variation results in more chance a few animals have exceptionally high reproductive potential and high survival. Therefore, these animals are unlikely to suffer mortality and be removed from the population, and also can be relied upon to contribute new births each year. As a result, the population may remain small, but will not go extinct as often. Individual heterogeneity has seldom, if ever, been included in a population viability analysis. Yet, as the simple example shows, individual heterogeneity is a very important element in maintaining viability.

Summary this far

Slide 23 of 47

Several lessons should be learned from this simple exercise. Persistence is a stochastic phenomena. Even though the expected outcome for a particular model is to persist, random variation prevents this outcome from always occurring. Small populations are much more likely to go extinct than larger populations because of demographic variation. Increased temporal variation results in decreased persistence. Increased individual variation results in increased persistence.

Components of a PVA

Slide 24 of 47

A basic population model is needed. A recognized mechanism of population regulation, density dependence, should be incorporated, because no population can grow indefinitely. “Of course, exponential growth models are strictly unrealistic on time scales necessary to explore extinction probabilities.” (Boyce 1992:489). The population cannot be allowed to grow indefinitely, or persistence will be over estimated. Further, as discussed below, the shape of the relationship between density and survival and reproduction and can affect persistence. Density dependence can provide a stabilizing influence that increases persistence in small populations.

Components of a PVA

Slide 25 of 47

Demographic variation must be incorporated in this basic model. Otherwise, estimates of persistence will be too high because the effect of demographic variation for small populations is not included in the model.

Components of a PVA

Slide 26 of 47

Temporal variation must be included for the parameters of the model, including some probability of a natural catastrophe. Examples of catastrophes are fires (e.g., Yellowstone National Park, USA, during 1988), hurricanes, typhoons, earth quakes, extreme drought or rainfall resulting in flooding, etc. Catastrophes must be rare, or else the variation would be considered as part of the normal temporal variation. However, the covariance of the parameters is also important. Good years for survival are likely also good years for reproduction. Vice versa, bad years for reproduction may also lead to increased mortality. The impact of this correlation of reproduction and survival can drastically affect results. For example, the model of Stacey and Taper (1992) of acorn woodpecker population dynamics performs very differently depending on whether adult survival, juvenile survival, and reproduction are bootstrapped as a triplet, or as individual rates across the 10 year period. By allowing the correlation of the survival rates and reproduction, persistence is improved.

Components of a PVA

Slide 27 of 47

Spatial variation in the parameters of the model must be incorporated if the population is spatially segregated. If spatial attributes are to be modeled, then immigration and emigration parameters must be estimated, as well as dispersal distances. The difficulty of estimating spatial variation is that the covariance of the parameters must be estimated as a function of distance, i.e., what is the covariance of adult survival of 2 subpopulations as a function of distance?

Components of a PVA

Slide 28 of 47

Individual heterogeneity must be included in the model. Individual heterogeneity requires that the basic model be extended to an individual-based model (DeAngelis and Gross 1992). As the variance of individual parameters increases in the basic model, the persistence time increases. Thus, instead of just knowing estimates of the parameters of our basic model, we also need to know the statistical distributions of these parameters across individuals. This source of variation is not mentioned in discussions of population viability analysis, e.g., Boyce (1992), Remmert (1994), Hunter (1996), Meffe and Carroll (1994), or Shaffer (1981, 1987).

Components of a PVA

Slide 29 of 47

For short-term projects, the above sources of variation may be adequate. However, if time periods of more than a few generations are projected, then genetic variation should be considered. I would expect the population to change as selection takes place. Even if no selection is operating, then genetic drift is expected for small population sizes. However, the importance of genetic effects is still an issue in question, e.g., Joopouborg and Van Groenendael (1996). Lande (1988, 1995) has suggested either demographic variation and/or genetic effects can be lethal to a small population.

Components of a PVA

Slide 30 of 47

For long-term persistence, we must be willing to make the assumption that the system will not change, i.e., the levels of stochasticity will not change through time, the species will not evolve through selection, and the supporting capacity of the environment (the species habitat) remains static. That is, natural processes such as long-term succession and climatic change do not affect persistence, and that humans cease and desist, given that humans have been responsible for most recent extinctions! To believe the results, we have to assume that the model and all its parameters stays the same across inordinately long time periods.

Process vs. Sampling Variation

Slide 31 of 47

The combined effects of demographic, temporal, spatial, and individual variation is termed €process variation€. That is, each of these sources of variation affect population processes. Process variation is used as a general term for the inherent stochasticity of changes in the population level. Process variation is in contrast to €sampling variation€, which is the variation contributed when biologists attempt to measure population processes. That is, researchers are unable to measure the exact survival rate of a population. Rather, they observe realizations of the process, but not the exact value. Even if the fate of every animal in the population is observed, the resulting estimate of survival is only an estimate of the true, but unknown, population survival rate. The concept of sampling variation will be elaborated on now, where methods of separating sampling variation from process variation will be developed.

Environmental Variation

Slide 32 of 47

The implication of the list of requirements for a PVA is that population parameters or their distributions are known without error, i.e., exact parameter values are observed, not estimated. In reality, we may be fortunate and have a series of survival or reproduction estimates across time that provides information about the temporal variation of the process. However, the variance of this series is not the proper estimate of the temporal variation of the process. This is because each of our estimates includes sampling variation, i.e., we only have an estimate of the true parameter, not its exact value. To properly estimate the temporal variation of the series, the sampling variance of the estimates must be removed. In this section, I demonstrate a procedure to remove the sampling variance from a series of estimates to obtain an estimate of the underlying process variation (which might be temporal or spatial variation). The procedure is developed in Burnham et al. (1987:260-278). Consider the example situation of estimating over-winter survival rates each year for 10 years from a deer population. Each year, the survival rate is different from the overall mean, because of snow depth, cold weather, etc. Let the true, but unknown, overall mean be S. Then the survival rate for each year can be considered to be S plus some deviation attributable to temporal variation.

Environmental Variation

Slide 33 of 47

In reality, we are never able to observe the annual rates because of sampling variation or demographic variation. For example, even if we observed all the members of a population, we would still not be able to say the observed survival rate was €S€i€€ because of demographic variation. Consider flipping 10 coins. We know that the true probability of a head is 0.5, but we will not always observe that value exactly. Imagine if you had 11 coins — the true value is not even in the set of possible estimates. The same process operates in a population as demographic variation. Even though the true probability of survival is 0.5, we would not necessarily see exactly � of the population survive on any given year.

Environmental Variation

Slide 34 of 47

The €e€i€€ are as before, but we also have additional variation from sampling variation, or demographic variation, or both, in the €f€i€€.

Environmental Variation

Slide 35 of 47

Environmental Variation

Slide 36 of 47

Environmental Variation

Slide 37 of 47

Example

Slide 38 of 47

Example Results

Slide 39 of 47

Indirect Estimation of Variation

Slide 40 of 47

Individual heterogeneity occurs in both reproduction and survival. Estimation of individual variation in reproduction is an easier problem than estimation of individual variation in survival because some animals reproduce more than once, whereas they only die once. Bartmann et al. (1992) demonstrated that over-winter survival of mule deer fawns is related to their weight at the start of the winter. Thus, one approach to modeling individual heterogeneity is to find a correlate of survival that can be measured, and develop statistical models of the distribution of this correlate. Then, the distribution of the correlate can be sampled to obtain an estimate of survival for the individual. €omnicki (1988) also suggests weight as an easily measured variable that relates to an animal’s fitness. Weight of fawns at the start of winter was approximately normally distributed with mean 32 kg and standard deviation 4.2. To simulate individual heterogeneity in over-winter fawn survival, values can be drawn from this normal distribution to generate survival estimates.

Bootstrap Approach

Slide 41 of 47

Stacy and Taper (1992) used a bootstrap procedure to incorporate temporal variation into a model of acorn woodpecker (€Melanerpes formicivorus€) population viability. They used estimates of adult and juvenile survival and reproductive rates resulting from a 10-year field study to estimate population persistence. To incorporate the temporal variation from the 10 years of estimates, they randomly selected with replacement 1 estimate from the observed values to provide an estimate in the model for a year. Randomly sampling estimates with a bootstrap procedure incorporates the sampling variation of the estimates into the persistence model. As a result of the increased variation, persistence values will be underestimated. Therefore, I suggest using sparingly the bootstrap approach demonstrated by Stacey and Taper (1992). Persistence estimates developed with this procedure will generally be too low, i.e., you will conclude the population is more likely to go extinct than it really will. However, methodologies such as shrinkage estimation of variances (K. P. Burnham, Pers. Commun.) may prove useful in removing sampling variance from the estimates, and make the bootstrap procedure more applicable to estimating population persistence.

Basic Population Model

Slide 42 of 47

Leslie matrix models (Leslie 1945, 1948; Usher 1966; Lefkovitch 1965; Caswell 1989; Manly 1990) are commonly used as the modeling framework for population viability models. Density dependence must be incorporated into the model, i.e., basic parameters must be a function of population size. Thus, the resulting model is not a true Leslie matrix. Each iteration of the calculation also requires a temporal variance component, and making the parameters of the Leslie matrix into random variables (Burgman et al. 1993) is the standard approach, but eradicates the analytical results that normally are benefits of Leslie’s creative work. If multiple patches are modeled, each patch requires a spatial variance component. Demographic variation can be built into the model. However, the resulting model doesn’t resemble the elegant matrix model that Leslie originally developed. However, use of the Leslie matrix framework ignores individual heterogeneity, and thus is likely to underestimate persistence. Incorporation of individual heterogeneity requires an individual-based model (e.g., DeAngelis and Gross 1992), and thus, is conceptually different from the basic Leslie matrix approach. Individual-based models can be spatially explicit (e.g., Conroy et al. 1995, Dunning et al. 1995, Holt et al. 1995, Turner et al. 1995), providing another approach to incorporating spatial stochasticity into the model.

Density Dependence

Slide 43 of 47

As suggested by Boyce (1992), Stacey and Taper (1992), and Burgman et al. (1993), density dependence is an important part of estimating a population’s persistence. Lande (1993) demonstrates that the importance of environmental stochasticity and random catastrophes depends on the density-dependence mechanism operating in the population based on the value of €K€ carrying capacity. However, how density dependence is incorporated into the model greatly affects the estimates of persistence. In persistence models, as a population declines, compensation for small population size takes the form of increased birth rates and decreased death rates (density dependence), and so is a significant factor in increasing population persistence. or € = 1, the 2 models are identical. Although Stacey and Taper’s data precluded a significant test between these models, their data did show significant correlations between adult survival and population size, suggesting that density dependence was operating in the population.

€-logistic Model

Slide 44 of 47

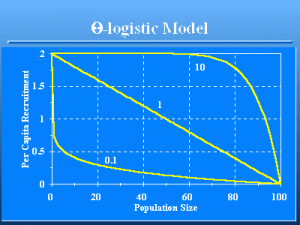
The distinction between the 2 models can be very important. In the first, the rate of change of the birth and death rates with population size is linear, i.e., the classic logistic population growth model. In the second, the change can be very nonlinear. As a result, the €-logistic model can cause populations to be very persistent, or very extinction prone, depending on the shape of the function. In Fig. 7, the curve for per capita recruitment with €€=€10 will result in a population with much greater persistence than the curve with €€=€0.1 because as the population size becomes small, the € = 10 population will be at peak reproduction for populations <60, whereas peak reproduction is only reached at a population size of zero for the �=”0.1″ population. Fowler (1981, 1994) argues that both theory and empirical information support the conclusion that most density-dependent change occurs at high population levels (close to the carrying capacity) for species with life history strategies typical of large mammals, such as deer (��> 1). The reverse is true for species with life history strategies typical of insects and some fishes, with € <1).

Allee Effect

Slide 45 of 47

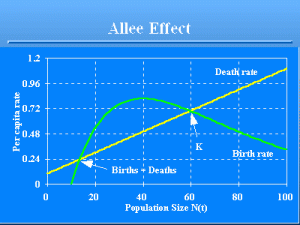
Another example of how density dependence can operate in small populations is provided by the Allee effect (Allee 1931), i.e., the per capita birth rate declines at low densities (Fig. 8) because, for example, of the increased difficulty of finding a mate (Yodzis 1989:12-13). This is known as €Allee-type behavior€ (of the per capita birth rate), and its effect on the per capita population growth rate, €R(t)€, is called an Allee effect. In theory, a low density equilibrium would be sustained in a deterministic equilibrium, where the birth rate equals the death rate. However, given stochasticity, the population could be driven below the low density equilibrium, and thus slide into extinction.

Problems with PVA

Slide 46 of 47

The real problem with PVA is not the model, but obtaining the data to drive the models (Ruggiero et al. 1994). Much of the published work on PVA ignores this essential (Thomas 1990). For example, Mangel and Tier (1994) simplify the process to the point that they miss major issues concerning data reliability and quality of the product (estimates of persistence). Conservation biologists would like to have “rules of thumb” to evaluate persistence (Boyce 1992), for example the magical Franklin-Soul� number of 500 (Franklin 1980, Soul� 1980) that is the effective population size (N_e) to maintain genetic variability in quantitative characters. Unfortunately, these rules lack the realism to be useful. The Franklin-Soul� number was derived from simple genetic models, and hence lacks the essential features of a PVA model discussed here. Attempts with simplistic models such as Mangel and Tier (1994) and Tomiuk and Loeschcke (1994) also do not provide defensible results because of the lack of attention to the biology of the species and the stochastic environment in which the population exists. Until conservation biologists do good experimental studies to evaluate population persistence empirically, I question the usefulness of “rules of thumb” and simplistic models suggested various places in the literature. In the meantime, until rigorous experimental work can be conducted, conservation biologists should borrow information from game species, where long-term studies have been done that will provide estimates of temporal and spatial variation and individual heterogeneity. Rules of thumb that predict temporal variation in survival as a function of weather, or individual variation in survival as a function of body characteristics, provide alternative sources of data.

Problems with PVA

Slide 47 of 47

In summary, most estimates of population viability are nearly useless because one or more of the following mistakes or omissions are made in developing a model to estimate persistence. 1. The model ignores spatial variation which will increase population viability. As suggested by Stacey and Taper (1992) immigration can occasionally rescue a population from extinction. 2. The model uses estimates of temporal variation that are at best, poor guesses. This statement assumes that the modeler understood the difference between process variation and sampling variation. Often, sampling variation is assumed to substitute for process variation, and, as a result, the estimates of persistence are useless. Sampling variation has nothing to do with population persistence. 3. The model uses demographic variation as a substitute for temporal variation in the process, and ignores true temporal variation. 4. The model ignores life-long individual heterogeneity that increases population viability, and assumes that all individuals endure the same identical survival and reproduction parameters. Such a naive assumption results in population viability being underestimated. 5. The model assumes that current conditions are not changing, i.e., the stochastic processes included in the model are assumed constant for the indefinite future. Loss of habitat and other environmental changes that affect these stochastic processes are ignored. Thus, as discussed by Caswell (1989), the model is likely not useful in forecasting (i.e., predicting what will happen), but is useful in projecting (i.e., predicting what would happen if conditions do not change).